
 Приоритет качества и профессионализма - Приоритет новых технологий - Приоритет Ваших интересов
Приоритет качества и профессионализма - Приоритет новых технологий - Приоритет Ваших интересов
 *
*
 *
*

|







|
|
|||||||


|
|||||||


|
|||||||


|
|||||||


|
|||||||


|
|||||||


|
|||||||

|
|||||||


|
|||||||
|
Оптимизация режимов работы системы, производящей однородную продукцию, без учёта транспортных расходовОглавление
ВведениеПусть есть система из некоторого количества узлов. Каждый узел производит некоторую одинаковую продукцию. Необходимо распределить заданную нагрузку по узлам так, чтобы суммарная стоимость была минимальна. Для каждого узла функция зависимости стоимости от количества продукции своя. Если эти функции выпуклы вниз, то метод решения этой задачи хорошо известен: метод последовательного приближения. В случае, если эти функции общего вида, то итерационные методы неприменимы. В этом случае задачу часто можно свести к целочисленной. Известно, что задачи целочисленного программирования (ЦП), как правило, являются NP-сложными ([5]). Развитие за последние 20 лет метода направленного перебора -- метода ветвей и границ (МВГ) и создание изощренных программ для ЭВМ (главным образом, коммерческих) в известной мере удовлетворили потребность в решении задач (частично) целочисленного программирования (ЦЛП/ЧЦЛП). Однако, возможности МВГ очень ограничены. Оставаясь в рамках МВГ, трудно рассчитывать на существенное увеличение размеров решаемых задач ЧЦЛП. Поэтому, он не применим для больших систем. В последнее время, разработан ряд методов улучшающих МВГ. Так, в 1998 году начались исследования метода узловых векторов (МУВ). Для задач средней размерности (до 80 целочисленных переменных) время решения по алгоритму МУВ оказалось в среднем в 2-5 раз меньше, чем по МВГ. К сожалению, этот метод не применим для систем из 1000 и более узлов. Алгоритм, представленный в данной работе, работает со скоростью метода последовательного приближения. С другой стороны, он работает для любых систем. Правда, метод даёт погрешность, но она меньше технической. Постановка задачиПусть есть узлов. Для каждого узла задана стоимостная характеристика Предварительные замечанияТакая постановка является довольно типичной. В частности, если узлы — это электрогенерирующие узлы,
то Обычно добавляется условие возрастания функций АлгоритмВведём обозначения. Для В начале итераций 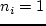
Проще говоря, В результате итераций мы построили последовательность точек Обоснование алгоритмаТеорема 1 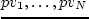
Значит задачу можно дискретизировать. Алгоритм даёт последовательность увеличений нагрузок на
станциях. Каждый шаг — это увеличение нагрузки Теорема 2 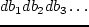
Это значит, что с каждым шагом увеличение нагрузки все менее выгодно. Ломаная Теорема 3 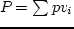
Теорема 4 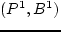
Погрешность алгоритмаЕсли график стоимости на узле выпуклый вниз, то к нему можно применить метод последовательных приближений. Однако если это не так, то надо применять другие методы. Описанный алгоритм в первом случае работает оптимально, а во втором работает с небольшой погрешностью. В результате итераций получается последовательность точек Теорема 4 показывает, что ломаная Если построить оптимальную кривую ЗаключениеДля большого числа узлов алгоритм работает очень быстро и даёт достаточно точный ответ. При малом числе узлов применим метод ветвей и границ. Для распределённых систем узлов можно применить комбинированный метод. Сначала для всей системы в целом применяется данный алгоритм. Далее для каждой небольшой автономной подсистемы результат можно улучшить с помощью метода ветвей и границ. Алгоритм описанный в данной работе представляет большой интерес для изучения оптимизации суточных диспетчерских графиков электрических и тепловых нагрузок энергообъектов. Поэтому, данная статья является частью более общего проекта. Он описан в [2]. Дальнейшие улучшения связаны с переходом от линейной апроксимации к сплайновой. Также важным является разделение продукции на несколько типов. Самым, пожалуй, важным является введение нового параметра — времени. Литература и гиперссылкиР. М. Беркович |
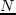 ,
где
,
где 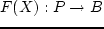 — продукция,
— продукция, 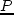 — стоимость. В общем случае
— стоимость. В общем случае
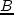 могут быть нетривиальными. В
данной работе обсуждается случай, когда
могут быть нетривиальными. В
данной работе обсуждается случай, когда 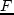 , а
, а 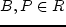 . Для заданного количества продукции нужно найти
распределение продукции по узлам так, чтобы суммарные затраты были минимальными. Формально: найти
. Для заданного количества продукции нужно найти
распределение продукции по узлам так, чтобы суммарные затраты были минимальными. Формально: найти 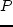 ,
где
,
где 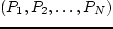 и
и 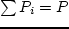 .
.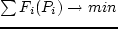 — минимальная и максимальная электронагрузка. (Задаются по технической характеристике
агрегата.) Условие кусочно-линейности стоимостной характеристики тоже легко объяснить. Хотя агрегат может работать в любой
точке отрезка
— минимальная и максимальная электронагрузка. (Задаются по технической характеристике
агрегата.) Условие кусочно-линейности стоимостной характеристики тоже легко объяснить. Хотя агрегат может работать в любой
точке отрезка 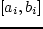 . Но если добавить к
каждой функции линейную
. Но если добавить к
каждой функции линейную 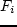 , то всегда можно добиться монотонности и положительности (и наоборот).
Поэтому это условие можно опустить.
, то всегда можно добиться монотонности и положительности (и наоборот).
Поэтому это условие можно опустить.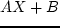 -ого узла точки, где известны стоимостные
характеристики, обозначим
-ого узла точки, где известны стоимостные
характеристики, обозначим 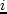 . Соответствующие стоимости обозначим
. Соответствующие стоимости обозначим 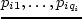 .
Ниже будет показано, что задачу можно дискретизировать: нагрузку можно выбирать из
.
Ниже будет показано, что задачу можно дискретизировать: нагрузку можно выбирать из  . Номер стоимостной
характеристики обозначим
. Номер стоимостной
характеристики обозначим 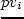 :
: 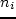 .
.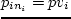 ,
, 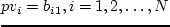 . Далее, на каждой
итерации для каждой станции строим массив приростов стоимости.
. Далее, на каждой
итерации для каждой станции строим массив приростов стоимости.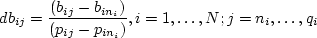 — это скорость роста (стоимость) затрат при увеличении
нагрузки на
— это скорость роста (стоимость) затрат при увеличении
нагрузки на 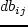 .
Дальше выбираем минимальное значение
.
Дальше выбираем минимальное значение 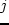 .
. 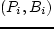 — суммарная продукция,
— суммарная продукция, 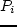 — суммарная стоимость после
— суммарная стоимость после 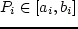 случайно совпало с одним
из
случайно совпало с одним
из 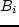 можно выбрать так,
что для всех узлов, кроме, быть может, одного,
можно выбрать так,
что для всех узлов, кроме, быть может, одного, 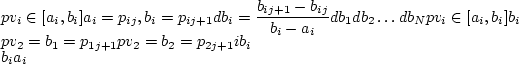 до
до
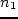 . Скорость изменения стоимости на
. Скорость изменения стоимости на 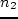 .
.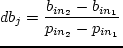 .
.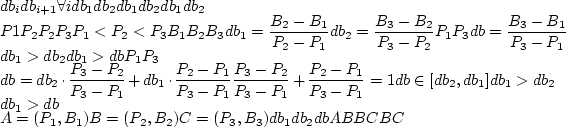 — выпукла вниз.
— выпукла вниз.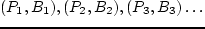 . Тогда для суммарной нагрузки
. Тогда для суммарной нагрузки 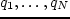 это распределение является оптимальным.
это распределение является оптимальным.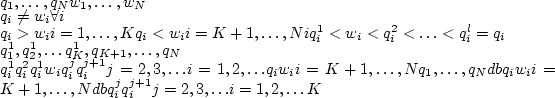 построим ломаную
построим ломаную 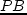 ,
, 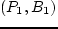 ,
,
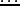 . Для произвольного значения
. Для произвольного значения 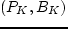 найдем оптимальное распределение
нагрузок с общей стоимостью
найдем оптимальное распределение
нагрузок с общей стоимостью 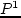 . Тогда точка
. Тогда точка 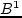 лежит выше ломаной.
лежит выше ломаной.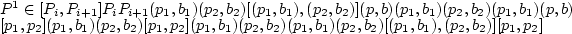 огибает все возможные распределения
снизу (по цене). Это даёт нижнюю границу. Теорема 2 говорит, что эта ломаная выпукла вниз.
огибает все возможные распределения
снизу (по цене). Это даёт нижнюю границу. Теорема 2 говорит, что эта ломаная выпукла вниз.